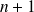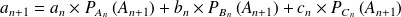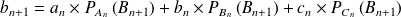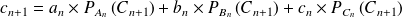Matrices et suites
Exemple : Étudier des suites à l'aide de matrices.
Considérons les suites définies par :
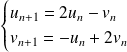avec
et
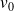deux réels.
On peut retranscrire ces informations à l'aide de trois matrices :
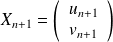
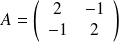
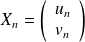
On a donc
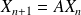
Fondamental : Matrice diagonalisable.
Une matrice carrée
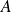d'ordre
est diagonalisable s'il existe une matrice
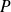carrée d'ordre
inversible telle que
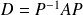où
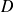est une matrice diagonale d'ordre
.
Vérifier pour notre exemple que la matrice
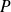convient :
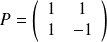
avec :
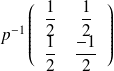
Vous devriez trouver que :
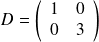
Méthode : Retour sur nos suites.
On a :
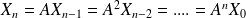
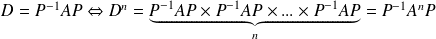
D'où :
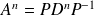
Et comme
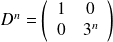
On en déduit que :
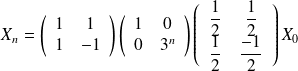
Vérifier que l'on obtient :
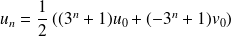
Qu'en est-il de
?
Exemple : Application aux probabilités-Marche aléatoire sur un graphe
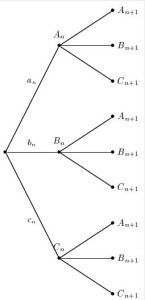
Un peu de théorie...Présentation dans le cas de matrices 3 x 3 :
Ω l'univers des possibles d'une expérience aléatoire
et A, B et C trois événements de Ω qui forment une partition de Ω. Une situation évolue en plusieurs étapes.
A chaque étape, on peut avoir soit A, soit B, soit C qui se produit.
Ce qui se traduit par un arbre pondéré entre les étapes
|  arbre |
On connaît bien sûr les 9 probabilités conditionnelles :
,
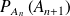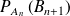etc.....
D'après la loi des probabilités totales on sait que :
Ce qui bien entendu peut se traduire par des matrices :
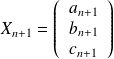
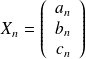
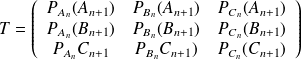
On a donc
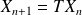
Et en supposant que T est diagonalisable, on peut écrire :
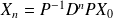
On pourra donc pour n'importe quelle étape connaître la probabilité que la situation se trouve dans l'état A,B ou C
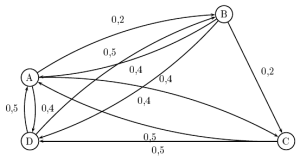
Exemple : Marche aléatoire sur un graphe.
Une fourmi se déplace sur les arêtes d'un tétraèdre régulier ABCD. Elle se déplace d'un sommet à un autre.
Initialement elle part du sommet A.
Elle parcourt successivement les arêtes de ce tétraèdre d'un sommet vers un autre sommet.
On note
,
,
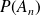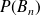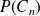et
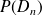la probabilité respective que le n-ième sommet qu'elle atteint soit A, B , C ou D.
On note
 graphe | On illustre la situation à l'aide d'un graphe probabiliste : |
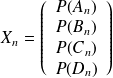
Méthode : Écrire la situation avec des matrices
La situation se réécrit de la façon suivante :
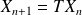où T est la matrice de transition d'un état à l'autre.
ici
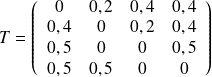
On sait que
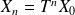. Quelle est la situation à l'étape 5 ? ( utiliser votre calculatrice ). A l'étape 50 ?
Exemple : Encore des suites
Suites du type
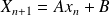
Un organisme de recensement étudie l'évolution de la population d'une certaine agglomération et notamment la répartition des habitants entre le centre-ville et la banlieue. On constate que tous les dix ans parmi les habitants du centre-ville, 20% partent habiter dans la banlieue, 75% restent en centre-ville et les derniers 5% résultent des départs vers d'autres villes et de la balance entre décès et naissances.
Tous les dix ans, parmi les habitants des banlieues 60 % continuent à habiter dans cette banlieue, 10 % vont habiter au centre-ville, les derniers 30% étant le fruit des déménagements hors agglomération et de l'évolution naturelle de la population.
De plus tous les dix ans, 5000 habitants venu de l'extérieur s'installent en banlieue et 2000 en centre-ville.
On note
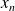et
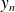respectivement la population de cette agglomération en centre-ville et en banlieue n décennies après le début de l'étude.
On note
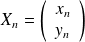
Montrer que la situation se transcrit à l'aide de matrice sous la forme :
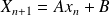
Déterminer deux réels a et b tels que la suite constante :
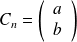vérifie la relation :
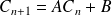soit
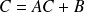
Pour tout
, on pose :
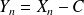, Montrer que
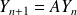.Démontrer alors que pour tout entier naturel n,
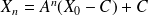.On constate qu'initialement le nombre d'habitants en centre-ville est de
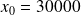et que le nombre d'habitants en banlieue est de
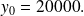
Déterminer en utilisant une calculatrice, combien d'habitants habiteront le centre-ville et combien habiteront la banlieue dans cette agglomération dans 50 ans.
En utilisant une calculatrice, conjecturer quels seront les coefficients de
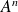lorsque n prend de grandes valeurs. Que peut-on en déduire pour
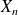à l'infini ?
