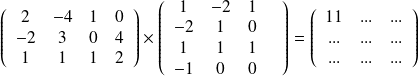Opérations sur les matrices
Addition-Soustraction
On ne peut additionner (soustraire) que des matrices de même taille.
Pour sommer deux matrices de même format, on additionne à chaque position leurs termes deux à deux.
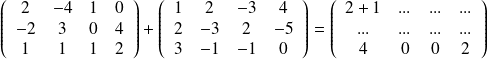
Faire la soustraction de ces deux matrices :
Multiplication par un réel.
Soient A une matrice et λ un réel, on calcule la matrice λ
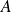est multipliant tous les termes de
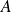par λ.
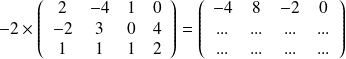
Exemple : Un petit calcul :
On considère les matrices
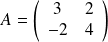et
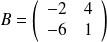
Calculer
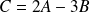
Le produit matriciel.
On considère une matrice ligne
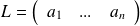et une matrice colonne
.
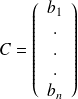Le produit
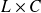noté
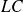est égal au réel
.
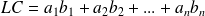Par exemple :
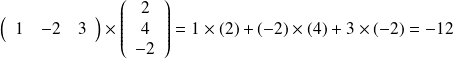
Définition : Produit de deux matrices.
On considère une matrice
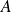de taille
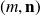et une matrice
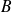de taille
.
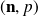Le produit AB est égal à la matrice C de taille (m, p) telle que le terme de position (i, j) de C est égal au produit de la i-ème ligne de A par la j-ème colonne de B.
Le produit de deux matrices n'existe que si le nombre de colonnes de la première est égal au nombre de lignes de la seconde. Ce qui signifie que le produit matriciel n'est pas commutatif
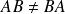: l'ordre de multiplication est important.
Exemple : calculer ce produit
