Les Matrices carrées.
Une matrice de taille
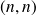, c'est-à-dire possédant n lignes et n colonnes, est appelée matrice carrée d'ordre n .
Attention : Propriétés
Soient
,
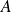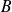et
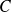trois matrices carrées d'ordre n, et λ un réel.
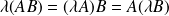
Associativité :
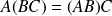
Distributivité :
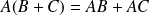et
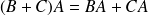
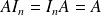
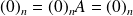
Piège
Deux matrices carrées
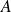et
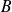d'ordre n commutent si et seulement si :
En général,
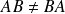
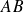peut être nulle sans que 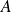ni
ni
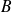ne soit nulle.
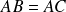n'implique pas nécessairement que
.
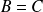Fondamental : Matrices diagonales
On considère deux matrices diagonales
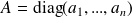et
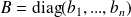. On a alors :
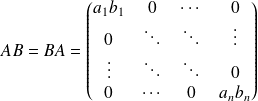
Attention : Les puissances
Soient
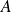une matrice carrée d'ordre n et k un entier naturel non nul, on définit les puissances de
:
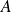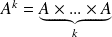
Par convention,
Pour tous entiers naturels non nuls k et r :
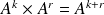
On considère une matrice diagonale
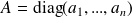et k un entier naturel non nul. On a :
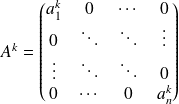
Définition : Inverse d'une matrice
La matrice carrée
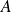d'ordre
est inversible si et seulement s'il existe une matrice
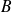telle que :
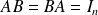
La matrice
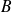est alors appelée matrice inverse de
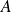et est notée :
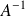, Elle est unique.
Exemple : Un exemple :
On considère les matrices
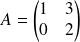et
.
.
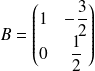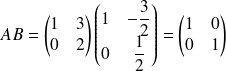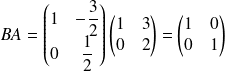
On en déduit que
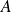est inversible et que
