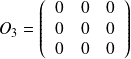Quelques définitions
Définition : Une matrice c'est quoi ?
Soient deux entiers naturels non nuls
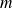et
. Une matrice
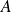de taille ou de format ou encore de dimension
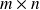est un tableau de réels composés de
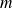lignes et de
colonnes.
Par exemple voici une matrice
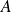de taille 4x3
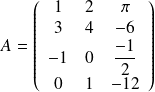
On note par exemple :
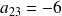ce qui signifie que le coefficient de la matrice
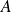se trouvant "à l'intersection" de la deuxième ligne et de la troisième colonne est
.
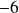En général..
De manière plus générale, on note une matrice
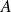de dimension
:
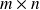Chaque coefficient
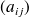étant bien sûr le coefficient de la ième ligne de la jème colonne.
Remarque : Du vocabulaire
Une matrice de taille
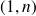, c'est-à-dire ne possédant qu'une seule ligne, est appelée matrice-ligne.
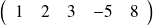
Une matrice de taille
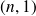, c'est-à-dire ne possédant qu'une seule colonne, est appelée matrice-colonne.
Une matrice de taille
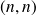, c'est-à-dire possédant
lignes et
colonnes, est appelée matrice carrée d'ordre n.
Les termes de positions
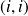d'une matrice carrée sont appelés coefficients diagonaux.La transposée d'une matrice
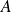de taille
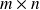est la matrice
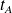de taille
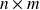dont les colonnes sont les lignes de
.
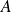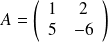donne
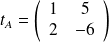
Exemple :
-
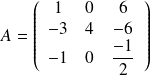
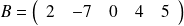
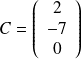
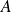est une matrice ...........d'ordre ..........
Le terme de position (1,3) est .........
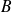est ............................................
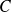est ...........................................
Attention : Égalité
Deux matrices sont égales si elles ont même taille et leur coefficients sont deux à deux égaux en toute position.
Fondamental : Matrice identité et matrice nulle
La matrice identité notée
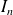d'ordre n est une matrice carrée dont les coefficients diagonaux valent tous 1 et les autres 0.
exemple :
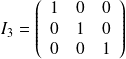
La matrice nulle notée
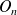d'ordre n est une matrice carrée dont les coefficients sont tous nul.
exemple :
