Opérations en binaire
Méthode : L'addition
 addition | L'addition en base 2 fonctionne comme l'addition que vous connaissez, sauf que ( 1 + 1 = 10, en fait 0 avec une retenue de 1). Exemple : prenons deux nombres : a = 21 = 00010101 et b = 25 = 00011001 codés sur 8 bits. En base 10 cela donne : a + b = 46 . En base deux cela donne : a + b = 00101110 ce qui fait bien 46. |
Si on ne dispose que de 8 bits, on ne pourra stocker le résultat d'une addition supérieure à 255.
Méthode : La multiplication.
Reprenons nos deux nombres a et b .
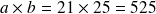
Or on ne peut pas obtenir 525 sur 8 bits, il faudra prévoir plus.....
 Multiplication | La méthode de multiplication est la même qu'en base 10 et attention aux retenues...( les lignes de 0 n'ont pas été écrites...) Il faudra au moins prévoir 10 bits pour stocker le résultat : 1000001101 |
Et les entiers négatifs ?
On pourrait coder des entiers "signés"en réservant un bit ( le 1er) pour signifier le signe.
par exemple +21= 00010101 et -21= 10010101.
Cela a le désavantage de fabriquer deux zéros ( +0 et -0 ).
La méthode que nous retiendrons est celle dite du " complément à 2 "
Attention : Le complément à 2
Soit
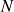un entier naturel codé en binaire sur 8 bits.
On note
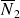le nombre tel que
.
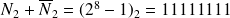Par exemple :
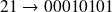qui donne
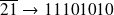
Un peu de mathématiques....
.
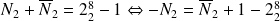Or
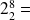100000000 qui sera interprété comme un zéro sur 8 bits car le 1 est sur le 9ème bit et ne sera pas pris en considération.
Ce qui nous amène à :
.
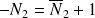Et donc
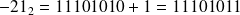
Ainsi
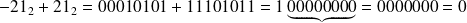sur 8 bits.
On retrouve un unique zéro et une méthode pour faire une soustraction.
Pour des nombres plus grand( N>255) il faut faire le complément à 2 sur un plus grand nombre de bits
Sur k bits le complément à 2 de N est
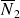et vérifie :
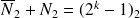
Et :
.
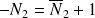Méthode : La soustraction.
Essayons la soustraction 25 - 21 = 4.
soit : 25+ (-21) = 00011001+11101011=
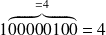sur 8 bits
Si on fait l'opération inverse : 21 - 25 on trouve 11111100 = 252 qui correspond bien au complément à 2 de 4=00000100.
et le résultat est bien -4.
