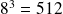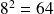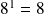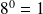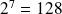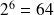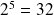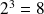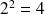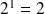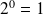Écriture en binaire d'un nombre entier
Bases de numération
Nous savons compter en base 10 depuis la maternelle, avec les chiffres 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Puis nous passons à 10, 11, 12 etc.
Il s'agit des mêmes chiffres avec une position en plus (les dizaines).
C'est ce qu'on appelle la numération décimale dite de position.
Nous aurions très bien pu ne compter qu'avec huit chiffres de 0 à 7.
Alors arrivé à 7, le 8 n'existant pas, on serait passé à 10, 11, ... 17, 20 ...
C'est la base 8 dite octale.
En base 2 ou binaire, on n'utilise que deux chiffres le 0 et le 1.
Arrivé à 1, le 2 n'existant pas, on passe à 10, 11, 100 ...
En base 12 (base duodécimale), nous utilisons les douze "chiffres" suivants: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B.
De sorte que, arrivé à B, nous passons à 10, 11, 12 ... 19, 1A, 1B, 20, 21 ...
En fait, le A en base 12 correspond au 10 en base décimale et le B correspond à 11.
En base 16 (hexadécimale), très utilisée en informatique, il faut utiliser 6 lettres-chiffres en plus des dix ordinaires.
décimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | ...... |
hexadécimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | ...... |
Fondamental : Principe de numération
Considérons un entier
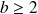, alors tout nombre entier
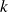peut s'écrire sous la forme :
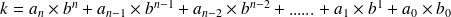
avec :
un entier naturel et les
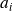des entiers naturels compris entre
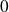et
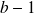
Par exemple, vérifiez avec votre calculatrice que :
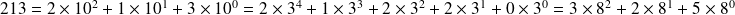
Notations : On note
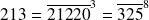ou bien
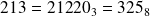
Sans précisions c'est la base 10 qui est sous entendue :
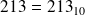
Méthode : Écrire en base 10 un nombre exprimé en base b
Pour passer de la base
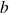à la base 10, il suffit d'écrire la décomposition en puissance de
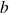et de la calculer.
Par exemple :
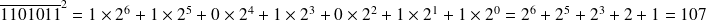
En Python il existe une méthode spéciale pour passer du binaire au décimal :
On fait précéder l'écriture par 0b
print(0b1101011)
Cette ligne affichera 107 dans la console
Méthode : Écrire en base b un nombre exprimé en base 10
Une première approche :
Prenons le nombre 213 et retrouvons son écriture en base 8.
Commençons par remplir un tableau avec les puissances de 8 en commençant par la droite :
..... |
|
|
|
|
Il est inutile d'aller plus loin car
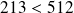
Comme
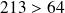, on peut savoir combien de fois il y a
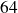dans
.
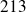Une simple division donne :
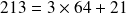
On place donc un 3 dans le tableau :
..... |
|
|
|
|
3 |
Il nous reste
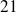
Comme
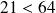mais supérieur à
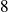, on recherche combien de fois il y a
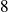dans
:
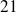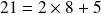
On complète le tableau :
..... |
|
|
|
|
3 | 2 |
Il reste 5 ( qui est inférieur à 8 )
On finalise le tableau :
..... |
|
|
|
|
3 | 2 | 5 |
Ainsi on obtient :
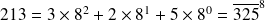
Un autre exemple : Écrivons 107 en binaire :
|
|
|
|
|
|
|
|
On a :
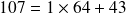
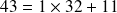
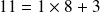
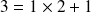
il reste
d'où le tableau :
|
|
|
|
|
|
|
|
1 | 1 | 0 | 1 | 0 | 1 | 1 |
On obtient donc :
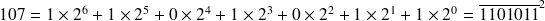
Fondamental : Comment ça marche ?
Une approche plus générale :
On souhaite écrire en base
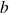un nombre entier
:
On effectue la division euclidienne de
par
:
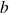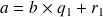
Puis on effectue la division euclidienne de
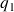par b ( si
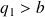sinon on a fini..)
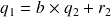que l'on injecte dans la première écriture :
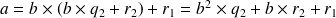
Maintenant si
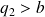, on recommence..
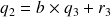
Ce qui donne :
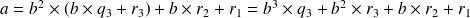
Et ainsi de suite jusqu'à ce que l'on ne puisse plus le faire
En observant le résultat, on remarque que :
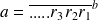
On peut donc s’affranchir des manipulations de calculs
Un exemple : 107 en binaire
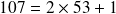
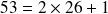
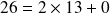
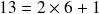
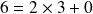
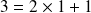
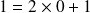
Donc en partant du dernier reste : 1101011
L'écriture en binaire de 107 est la suite des restes en commençant par le dernier :
1101011
Simulation : Avec Python
En python pour voir l'écriture d'un entier en base 2, 8 ou 16 il suffit d'écrire ces lignes :
print(bin(107))
print(oct(213))
print(hex(1512))
On obtient dans la console :
0b1101011
0325
000005E8
Attention : Nombres de bit nécessaires pour coder des entiers en binaire
Supposons que nous ayons 4 bits à notre disposition (4 'places' dans une mémoire)
Le plus grand entier que nous pouvons coder est :
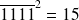soit les
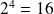premiers entiers
Pour 8 bits les
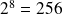premiers entiers
Pour 32 bits les
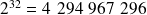
Et pour 64 bits.....
