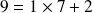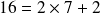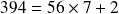Les congruences
Découvrir.
Dans la division euclidienne d'un entier par
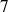 , les restes possibles sont
, les restes possibles sont
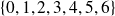
Par exemple :
Ainsi les nombres
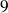 ,
,
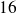 et
et
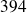 ont même reste dans la division euclidienne par
ont même reste dans la division euclidienne par
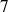 .
.
On dit qu'ils sont congrus entre eux modulo
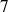 .
.
Cela se note :
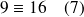 ou encore
ou encore
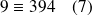 .
.
Congru à 0 | Congru à 1 | Congru à 2 | Congru à 3 | Congru à 4 | Congru à 5 | Congru à 6 |
|---|---|---|---|---|---|---|
0 | 1 | 2 | 3 | 4 | 5 | 6 |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
... | ... | ... | ... | ... | ... | ... |
392 | 393 | 394 | 395 | 396 | 397 | 398 |
399 | 400 | 401 | 402 | 403 | 404 | 405 |
... | ... | ... | ... | ... | ... | ... |
Dans la première colonne on remarque qu'il s'agit des multiples de
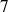 .
.
Définition : Congruences.
Soient
 et
et
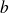 deux entiers relatifs et
deux entiers relatifs et
 un entier naturel non nul.
un entier naturel non nul.
On dit que
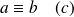 si et seulement si
si et seulement si
 et
et
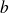 ont même reste dans la division euclidienne par
ont même reste dans la division euclidienne par
 .
.
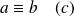 se lit
se lit «
 est congru à
est congru à
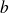 modulo
modulo
 »
»
Par exemple :
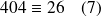
Fondamental : Congruence et divisibilité.
Prenons par exemple,
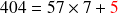 et
et
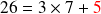 .
.
Leur différence
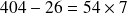 est un multiple de
est un multiple de
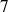 .
.
De manière plus générale, considérons deux entiers
 et
et
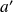 et un entier naturel non nul
et un entier naturel non nul
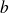 .
.
Or
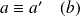 équivaut à dire qu'ils ont même reste dans la division euclidienne par
équivaut à dire qu'ils ont même reste dans la division euclidienne par
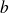 .
.
Soit :
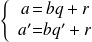 .
.
Et donc :
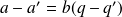 , c'est-à-dire que
, c'est-à-dire que
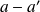 est un multiple de
est un multiple de
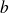 .
.
Ou encore que
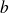 divise
divise
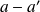 .
.
________________________________________________________________________________________________________
Ce qu'il faut retenir :
Soient
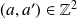 et
et
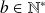 .
.

Exemple : Montrons que tous les nombres pairs sont congrus entre eux modulo 2.
Les nombres pairs sont des multiples de
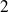 .
.
Prenons deux nombres pairs :
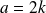 et
et
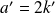 , pour
, pour
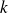 et
et
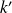 deux entiers relatifs non nuls.
deux entiers relatifs non nuls.
Or
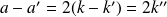 est un multiple de
est un multiple de
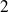 donc
donc
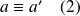 .
.
Et les nombres impairs ?
Attention : Propriétés.
Propriété 1 : Tout entier est congru à son reste modulo
 , dans la division euclidienne par
, dans la division euclidienne par
 .
.
Soit
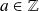 et
et
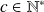 .
.

Exemple :
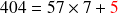 donc
donc
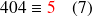
Preuve :
![]()
Comme
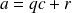 , on a :
, on a :
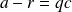 ce qui équivaut à :
ce qui équivaut à :
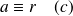 .
.
![]()
Propriété 2 :
Si
 est un multiple de
est un multiple de
 alors
alors
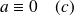
Exemple :
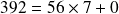 donc
donc
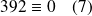 .
.
Preuve :
![]()
On a :
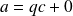 donc
donc
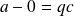 d'où :
d'où :
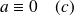 .
.
![]()
Propriété 3 :

Soient
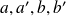 quatre entiers relatifs et
quatre entiers relatifs et
 un entier naturel non nul.
un entier naturel non nul.
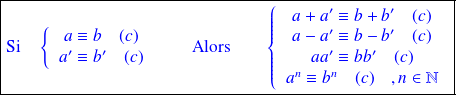
Preuves :
![]()
On en présente une en exemple, les autres se font à peu près de la même manière.
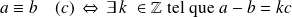 .
.
De même
 .
.
Donc des égalités :
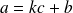 et
et
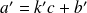 il vient par exemple
il vient par exemple
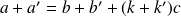 soit
soit
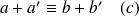 .
.
Pour
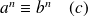 une récurrence semble s'imposer !
une récurrence semble s'imposer !