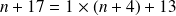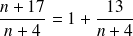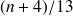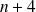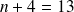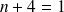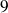Divisibilité dans l'ensemble des entiers relatifs.
L'ensemble des entiers naturels se note :
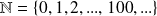
L'ensemble des entiers relatifs se note :
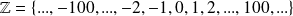
Définition : Définition 1
Soient
 et
et
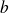 deux entiers relatifs non nuls.
deux entiers relatifs non nuls.
Si il existe un entier relatif
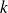 non nul tel que
non nul tel que
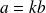 , on dit alors que :
, on dit alors que :
 est un multiple de
est un multiple de
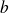 .
.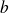 est un diviseur de
est un diviseur de
 .
.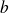 divise
divise
 et cela se note :
et cela se note :
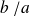 .
.
Exemple :
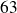 est multiple de
est multiple de
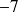 .
.
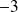 divise
divise
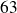 .
.
Les diviseurs de
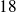 sont
sont
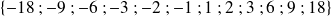
Les diviseurs de
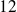 sont
sont
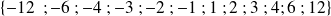
Leurs diviseurs communs sont :
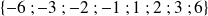
Remarque : Quelques remarques utiles.
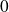 est multiple de tout entier.
est multiple de tout entier.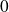 ne divise aucun entier et n'a qu'un seul multiple (lui-même).
ne divise aucun entier et n'a qu'un seul multiple (lui-même).Tout entier admet un nombre fini de diviseurs.
Tout entier admet une infinité de multiples.
Définition : Nombres premiers entre eux.
Deux entiers sont dits premiers entre eux si et seulement si leurs seuls diviseurs communs sont
 et
et
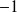 .
.
Ainsi
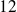 et
et
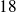 ne sont pas premiers entre eux.
ne sont pas premiers entre eux.
Méthode : Divisons...
Comment déterminer les entiers naturels
 ( s'ils existent ) pour lesquels le nombre
( s'ils existent ) pour lesquels le nombre
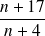 est un entier naturel ?
est un entier naturel ?
Une division "à la main" nous permet d'écrire que :
Pour obtenir un entier il faut donc que
Soit que :
C'est-à-dire que :
Soit
Donc le seul entier naturel
| 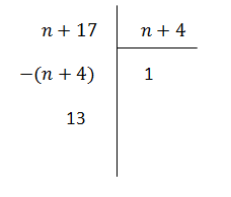 Division |
Si maintenant on recherche les entiers relatifs
 pour lesquels la fraction
pour lesquels la fraction
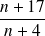 est entière et à condition que
est entière et à condition que
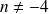 , il y a quatre solutions possibles
, il y a quatre solutions possibles
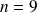 ,
,
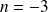 ,
,
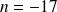 et
et
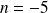 .
.
En effet, les diviseurs de
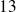 sont
sont
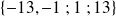 .
.
Exemple : Même problème avec :
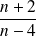 .
.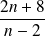 .
.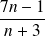 .
.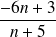 .
.Un peu plus compliqué :
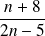 .
.
Méthode : Factorisons...
Comment déterminer les couples
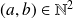 pour lesquels :
pour lesquels :
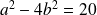 ?
?
Cette égalité équivaut à :
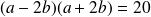 .
.
Comme
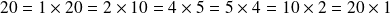 ;
;
On obtient
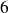 systèmes :
systèmes :
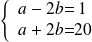 qui donne par addition :
qui donne par addition :
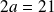 ce qui n'admet pas de solutions dans
ce qui n'admet pas de solutions dans
 .
.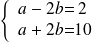 dont la solution est le couple
dont la solution est le couple
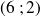 .
.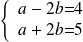 impossible dans
impossible dans
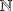 .
.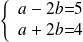 impossible dans
impossible dans
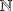 .
.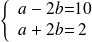 impossible dans
impossible dans
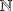 .
.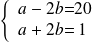 impossible dans
impossible dans
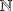 .
.
L'unique couple solution est donc
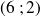 .
.
Qu'en est-il dans
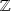 ?
?
Exemple : Même questions avec :
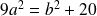 .
.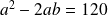 .
.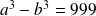 .
.
Fondamental : Propriétés
Propriété 1 :
 ,
,
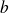 et
et
 trois entiers relatifs avec
trois entiers relatifs avec
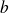 et
et
 non nuls.
non nuls.
Si
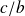 et
et
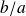 alors
alors
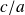 .
.
Preuve :
![]()
Si
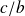 alors
alors
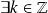 tel que
tel que
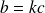 .
.
De même
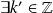 tel que
tel que
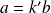 .
.
Et en substituant
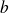 on obtient :
on obtient :
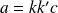 ce qui est entraîne bien que
ce qui est entraîne bien que
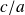
___________________________________________________________
Propriété 2 :
 ,
,
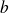 et
et
 trois entiers relatifs avec
trois entiers relatifs avec
 non nul.
non nul.
Si
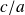 et
et
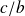 alors
alors
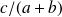 et
et
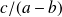 .
.
Preuve :
![]()
Si
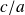 alors
alors
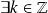 tel que
tel que
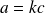 .
.
De même
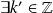 tel que
tel que
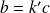 .
.
On a alors :
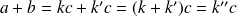
Et donc :
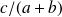 ;
;
C'est le même raisonnement pour
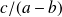 .
.
____________________________________________________________
Propriété 3 :
C'est une généralisation de la précédente. Si
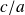 et
et
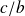 alors
alors
 divise toute combinaison linéaire de
divise toute combinaison linéaire de
 et
et
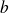 .
.
Soit
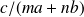 pour tout couple
pour tout couple
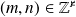 .
.
Preuve :
On pratique comme précédemment. ( c'est un bon entraînement de le faire ).