Chapitre 7
Programmation dynamique
------------------------------ Chapitre réalisé d'après le travail du très dynamique David Roche ------------------------------
La suite de Fibonacci
1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - ......
On a : u1 = 1 , u2 = 1
Puis : un= un-1 + un-2
Un programme itératif
La fonction ci-dessous calcule le terme un de la suite de Fibonacci :
Une version récursive
Le fait que la suite de Fibonacci soit définie de manière récurrente suggère qu'une version récursive de cette fonction se décline comme suit
fib(n) = fib(n-2) + fib(n-1)
Voici l'algorithme :
-----------------------------------------------------------------------------------------------
fonction fibo_recursif(n) :
Si n < 2 :
Renvoyer 1
Sinon :
Renvoyer fibo_recursif(n-2) + fibo_recursif(n-1)
-------------------------------------------------------------------------------------------------
À faire 1 : implémenter cet algorithme et le tester.
Voici une illustration du fonctionnement de ce programme pour n = 6 :
En additionnant les résultats de toutes les feuilles on trouve bien 13 (fib(1)=fib(0)=1).
En y regardant de plus près, on remarque que de nombreux calculs sont effectués plusieurs fois, comme le calcul de fib(4).
Le calcul pourrait être simplifié en mémorisant la valeur de fib(4) pour la réutiliser.
Voici l'algorithme qui réalise cette simplification :
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
n est un entier naturel
On dispose d'un tableau t contenant n+1 zéros
fonction fibo_dynamique(n,t) :
Si n < 2 :
On mémorise à l'indice n la valeur de n dans le tableau (t[n] <-- n )
Renvoyer 1
Sinon Si t[n] n'est pas nul :
Renvoyer t[n] (le terme de la suite est déjà calculé)
Sinon :
t[n] <-- fibo_dynamique(n-2,t) + fibo_dynamique(n-1,t) (on mémorise le résultat dans le tableau à l'indice n)
Renvoyer t[n]
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
À faire 2 : implémenter cet algorithme et le tester.
Dans le cas qui nous intéresse, on peut légitimement s'interroger sur le bénéfice de cette opération de "mémorisation", mais pour des valeurs de n beaucoup plus élevées, la question ne se pose même pas, le gain en termes de performance (temps de calcul) est évident.
Pour des valeurs n très élevées, dans le cas du programme récursif "classique" (n'utilisant pas la "mémorisation"), on peut même se retrouver avec un programme qui "plante" à cause du trop grand nombre d'appels récursifs.
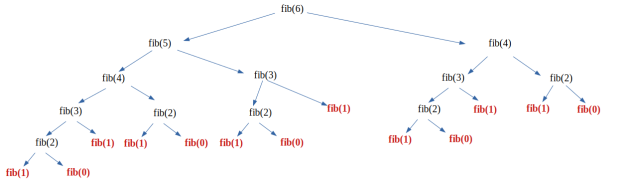
Pour calculer fib(6), on divise le problème en sous problèmes jusqu'à résoudre des problèmes simples (fib(0) et fib(1)).
Nous pouvons supposer qu'il s'agit là de la méthode "diviser pour régner".
Cependant dans cette dernière la mémorisation des calculs n'est pas prévue.
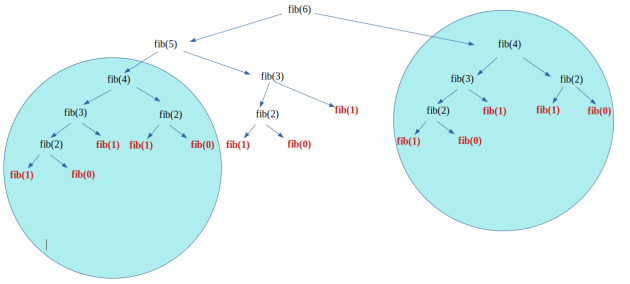
La méthode qui consiste à mémoriser les calculs se nomme programmation dynamique.
Programmation dynamique
Comme nous venons de le voir, la programmation dynamique, comme la méthode diviser pour régner, résout des problèmes en combinant des solutions de sous-problèmes.
Cette méthode a été introduite au début des années 1950 par Richard Bellman.
La programmation dynamique s'applique généralement aux problèmes d'optimisation. Nous avons déjà évoqué les problèmes d'optimisation lorsque nous avons étudié les algorithmes gloutons l'année dernière.
Comme déjà évoqué plus haut, à la différence de la méthode diviser pour régner, la programmation dynamique s'applique quand les sous-problèmes se recoupent, c'est-à-dire lorsque les sous-problèmes ont des problèmes communs (dans le cas du calcul de fib(6) on doit calculer 2 fois fib(4).
Pour calculer fib(4), on doit calculer 4 fois fib(2)...).
Un algorithme de programmation dynamique résout chaque sous-sous-problème une seule fois et mémorise sa réponse dans un tableau, évitant ainsi le recalcul de la solution chaque fois qu'il résout chaque sous-sous-problème.
