Représenter un nombre réel
Coder un nombre réel.
En informatique un réel est en fait un décimal....Nous sommes limités par le nombre de bits que nous réservons pour coder un nombre.
Considérons le nombre
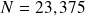, il est constitué d'une partie entière et d'une partie décimale.
En base 10 le nombre 23,375 se réécrit comme suit :
23,375 = 2x 10 +3 x 1 + 3 x 0,1 + 7 x 0,01 + 5 x 0,001...ce qui revient à écrire:
23,375 = 2 x 101 + 3 x 100 + 3 x 10-1 + 7 x 10-2 + 5 x 10-3
En base 2 le nombre 10111,011 se réécrit comme suit :
10111,011 = 1 x 24 + 0 x 23 + 1 x 22 + 1 x 21 + 1 x 20 + 0 x 2-1 + 1 x 2-2 + 1 x 2-3 ...soit:
10111,011 = 1 x 16 + 0 x 8 + 1 x 4 + 1 x 2 + 1 x 1 + 0 x 0,5 + 1 x 0,25 + 1 x 0,125
...c'est-à-dire 10111,0112 = 23,37510
Méthode : Comment ça marche ?
On vient de voir que : 10111,0112 = 23,37510
Pour coder 23 en binaire c'est la méthode utilisée pour coder un nombre entier. 2310 =101112
Pour coder 0,375 on utilise la méthode suivante :
0,375 x 2 = 0,750 ....... ( ce qui signifie que : 0,375 = 0,750 x 2-1 =0 x 2-1 + 0,75 x 2-1).
O,750 x 2 = 1,5 ...........( ce qui signifie que : 0,75 = 1,5 x 2-1 soit encore que : ( 0,375 =0 x 2-1 + ( 1,5 x 2-1 ) x 2-1 =0 x 2-1 + 1,5 x 2-2 = 0 x 2-1 + 1 x 2-2 + 0,5 x 2-2 ).
O,5 x 2 = 1 .................( ce qui signifie que : 0,5 = 1 x 2-1 soit encore que : ( 0,375 =0 x 2-1 + 1 x 2-2 + ( 1 x 2-1 ) x 2-2 = 0 x 2-1 + 1 x 2-2 + 1 x 2-3 = 0,0112 ).
0n obtient ainsi : 23,37510 = 10111,0112 .
Cependant la virgule n'est pas codée....
Tout comme 23,375=2,375 x 10 1 on peut écrire 10111,0112=1,0111011 x 242
Cette méthode permet de normaliser la position de la virgule.
C'est ce que l'on appelle la notation en virgule flottante.
Pour coder un nombre réel sur 32 bits, on utilise le fait que :
Tout nombre réel en base 2 peut s'écrire sous la forme
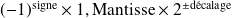
Et pour ne pas avoir à traiter les signes négatifs dans "décalage" , on lui ajoute 127
Ce qui donne :
Sur 32 bits on obtient l'écriture :
1 bit pour le signe (0 ou 1) à gauche
8 bits pour l'exposant ( décalage + 127 )
23 bits pour la mantisse
Pour 23,375
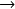10111,0112=1,0111011 x 242
Le signe : 0 ici car c'est un nombre positif
L'exposant : 4
4+127 = 131 qui se code en binaire par : 10000011La mantisse : Il faut la compléter par des 0 pour qu'elle occupe les 23 bits : 011101100000000000000000
Signe | Exposant | Mantisse |
|---|---|---|
0 | 10000011 | 011101100000000000000000 |
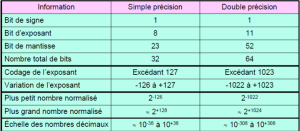
Codage en simple ou double précision
Pour augmenter la précision il suffit d'étendre le nombre de bit réservé à l'exposant et à la mantisse |  |
Exemple : Décodons un nombre..
Signe | Exposant | Mantisse |
|---|---|---|
1 | 10000100 | 10110100000000000000000 |
Il est négatif
L'exposant : 10000100
132
132-127=5
Donc :
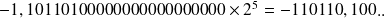
110110
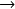540,1 donne
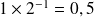
Le nombre cherché est donc : -54,5
Complément : Précisions sur le codage des réels...
Comme on l'a vu, en informatique tout nombre réel est un décimal ( par la limitation du nombre de bits )
Un décimal est un nombre qui s'écrit sous la forme :
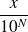, ou
est un entier relatif et
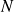un entier naturel
Par exemple :
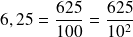
Les nombres dyadiques
Un nombre est dyadique s'il peut s'écrire sous la forme
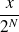, ou
est un entier relatif et
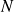un entier naturel
Par exemple :
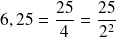
On ne peut représenter ( en binaire ) exactement que des nombres dyadiques
La représentation en binaire de
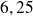donne :
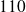pour le
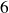
Pour la partie décimale :
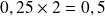( on retient 0)
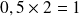(on retient 1)
Ce qui donne
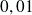
On obtient donc :
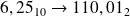
Le fait qu'il soit dyadique entraîne que sa partie décimale en binaire est finie ( le calcul s’arrête )
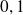n'est pas un nombre dyadique
Sa représentation en binaire est :
Il y a une répétition à l'infini de
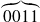
Sa représentation en binaire ne sera qu'une approximation de
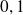
Conséquences :
En informatique, l'égalité entre nombres flottants n'a pour ainsi dire aucun sens puisque les écritures peuvent être infinies
Par exemple, si vous testez cette égalité :
print(0.1 + 0.1 + 0.1 == 0.3)
La réponse sera : False
Pour comparer de façon raisonnable deux flottants, on fera intervenir une marge d'erreur
Par exemple, ci-dessous, on choisit une marge d'erreur en considérant que toute quantité inférieure à
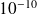est nulle
print(0.1+0.1+0.1-0.3<=10e-10)
La réponse dans ce cas est : True
