Les nombres premiers
Définition

0 n'est pas premier (il admet une infinité de diviseurs).
1 n'est pas premier (il n'admet qu'un seul diviseur).
2, 3, 5, 7, .... sont premiers.
Fondamental : Théorème
Soit un entier naturel

 admet au moins un diviseur premier.
admet au moins un diviseur premier.Si n n'est pas premier, alors
 admet au moins un diviseur premier
admet au moins un diviseur premier
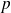 tel que
tel que
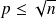 .
.
__________________________________________________
Preuve :
1ercas :
 est premier.
est premier.
Il est clair que
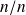 , donc
, donc
 admet bien un diviseur premier.
admet bien un diviseur premier.
2ème cas :
 n'est pas premier.
n'est pas premier.
Alors
 admet au moins un diviseur
admet au moins un diviseur
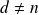 et
et
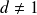 .
.
![]()
Donc l'ensemble des diviseurs de
 autre que
autre que
 et
et
 n'est pas vide et fini (cela signifie qu'il contient un nombre fini d'éléments).
n'est pas vide et fini (cela signifie qu'il contient un nombre fini d'éléments).
Cet ensemble admet donc un plus petit élément, que nous noterons
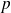 .
.
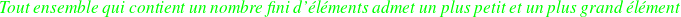
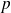 est nécessairement premier, car si on suppose le contraire, il admet alors lui même un diviseur premier
est nécessairement premier, car si on suppose le contraire, il admet alors lui même un diviseur premier
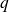 avec
avec
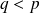
On aurait alors
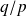 et
et
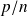 donc
donc
 ce qui n'est pas possible puisque
ce qui n'est pas possible puisque
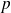 est le plus petit des diviseurs de
est le plus petit des diviseurs de
 .
.
De plus : Comme on sait
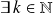 tel que
tel que
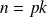 avec
avec
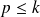
On a donc :
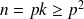 ce qui entraîne que
ce qui entraîne que
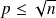 .
.
Exemple : Application
Les nombres
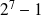 et
et
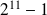 sont-ils premiers ?
sont-ils premiers ?
Fondamental : Théorème

__________________________________________________
Preuve :
Supposons qu'il y ait un nombre fini de nombres premiers.
Notons
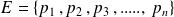 l'ensemble de tous les nombres premiers.
l'ensemble de tous les nombres premiers.
Considérons maintenant le nombre
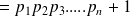
![]()
1ercas :
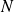 est premier, on a donc trouvé un nombre premier qui n'est pas dans
est premier, on a donc trouvé un nombre premier qui n'est pas dans
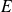 , ce qui contredit l'hypothèse faite.
, ce qui contredit l'hypothèse faite.
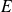 contient donc une infinité d'éléments.
contient donc une infinité d'éléments.
2ème cas :
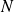 n'est pas premier.
n'est pas premier.
Il admet donc un diviseur
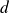 premier.
premier.
Or avec notre hypothèse,
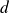 est l'un des
est l'un des
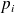 .
.
Donc
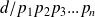 et
et
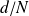 donc
donc
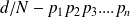 .
.
Donc
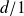 donc
donc
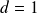 .
.
Ce qui n'est pas possible puisque
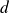 est premier.
est premier.
Donc
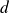 est un nombre premier qui n'est pas dans
est un nombre premier qui n'est pas dans
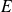 .
.
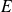 contient donc une infinité d'éléments.
contient donc une infinité d'éléments.
Fondamental : Théorème
Décomposition d'un entier naturel en produit de facteurs premiers.

Exemple :
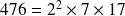
__________________________________________________
Preuve : Existence
Soit
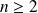 un entier.
un entier.
![]()
 admet donc un diviseur premier
admet donc un diviseur premier
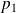 , donc
, donc
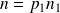 .
.
Deux cas sont possibles :
1ercas :
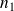 est premier et
est premier et
 se décompose bien en un produit de facteurs premiers .
se décompose bien en un produit de facteurs premiers .
2ème cas :
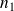 n'est pas premier,
n'est pas premier,
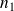 admet donc un diviseur premier
admet donc un diviseur premier
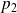 , d'où
, d'où
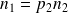 .
.
Et donc
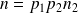 .
.
Deux cas sont à nouveau possibles :
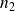 premier ou pas...
premier ou pas...
Et ainsi de proche en proche on montre que
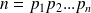 où les
où les
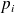 sont des nombres premiers non nécessairement tous distincts.
sont des nombres premiers non nécessairement tous distincts.
Remarque : Cette suite de nombres entiers
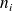 s'arrête nécessairement car elle est décroissante et minorée par
s'arrête nécessairement car elle est décroissante et minorée par
 .
.
__________________________________________________
Donc en regroupant les facteurs entre eux on peut écrire que :
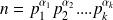 où les
où les
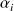 sont des entiers naturels non nuls.
sont des entiers naturels non nuls.

Voilà un programme pour Casio qui décompose un entier en produit de facteurs premiers.
"N=" : ?
2->k ( on met 2 dans la variable k )
n->m
m^0.5->r
While m>1
if mod(m,k)=0 ( ou m-k*Int(m/k)=0 )
then
Print k ( k suivi du triangle noir )
m/k=->m
m^0.5->r
else
k+1->k
if k>r
m->k
IfEnd
IfEnd
WhileEnd
Le même pour des TI.
Prompt n (ou Input)
2->k:
n->m
m^0.5->r
While (m>1)
if mod(m,k)=0 ( ou m-k*Int(m/k)=0 )
then
disp k
m/k->m
m^0.5->r
else
k+1->k
if k>r
m->k
Endif
Endif
Endwhile
Complément : Application à la recherche de diviseurs
Soit
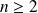 un entier naturel.
un entier naturel.
On sait que :
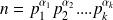 .
.
Alors les diviseurs de
 sont de la forme :
sont de la forme :
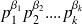 où
où
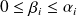
____________________________________________________
De plus :
Si
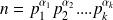 ,
,
 admet
admet
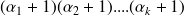 diviseurs.
diviseurs.
Par exemple :
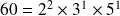 admet
admet
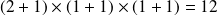 diviseurs.
diviseurs.
Exemple : Application
Exemple 1 :
Un entier naturel admet 5 diviseurs positifs. Quel peut être cet entier ?
Notons
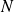 cet entier.
cet entier.
On sait qu'il se décompose en un produit de facteurs premiers :
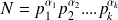 avec
avec
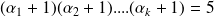 .
.
Ce qui entraîne que l'un des
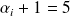 et que les autres valent 1.
et que les autres valent 1.
Soit l'un des
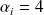 et les autres valent 0.
et les autres valent 0.
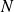 est donc la puissance 4ème d'un nombre premier.
est donc la puissance 4ème d'un nombre premier.
_______________________________________________________________
Exemple 2 :
Quel est le plus petit entier naturel admettant 12 diviseurs positifs ?
De la même manière on obtient :
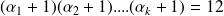
En supposant les
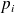 rangés dans l'ordre croissant. (
rangés dans l'ordre croissant. (
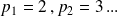 ).
).
On a les cas suivants :
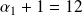 et les autres valent 1.
et les autres valent 1.
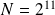
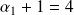 ,
,
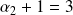 et les autres valent 1.
et les autres valent 1.
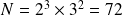
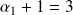 ,
,
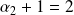 ,
,
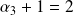 et les autres valent 1.
et les autres valent 1.
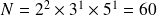 . (le plus petit)
. (le plus petit)etc...





