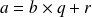La division Euclidienne.
La division Euclidienne dans l'ensemble des entiers naturels
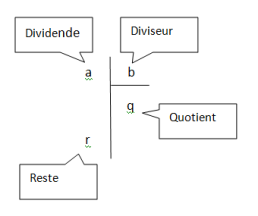 La division | Une fois la division effectuée on peut écrire que :
|
Fondamental : Théorème
Soient
 et
et
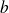 deux entiers naturels avec
deux entiers naturels avec
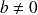 , il existe un unique couple
, il existe un unique couple
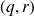 d'entiers naturels tels que
d'entiers naturels tels que
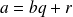 avec
avec
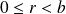 .
.
Preuve : Existence.
![]()
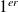 cas :
cas :
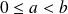 , le couple
, le couple
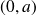 convient .
convient .
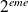 cas :
cas :
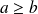 :
:
Considérons
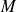 l'ensemble des multiples de
l'ensemble des multiples de
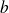 .
.
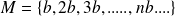 , Cet ensemble est infini.
, Cet ensemble est infini.
Et comme
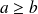 ,
,
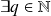 pour lequel
pour lequel
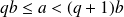 .
.
On pose
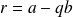 , et on a bien :
, et on a bien :
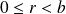 avec
avec
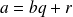 .
.
Preuve : Unicité.
![]()
Supposons l'existence de deux couples
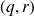 et
et
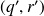 tels que :
tels que :
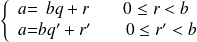 .
.
En égalisant ces deux écritures de
 , on obtient :
, on obtient :
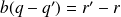 , ce qui entraîne que
, ce qui entraîne que
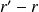 est un multiple de
est un multiple de
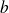 .
.
En additionnant les deux inégalités membre à membre :
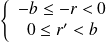 .
.
On obtient :
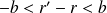 , donc
, donc
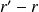 est un multiple de
est un multiple de
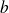 plus petit que
plus petit que
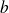 , ce ne peut être que
, ce ne peut être que
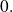
D'où
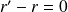 soit
soit
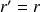 .
.
Ce qui entraîne bien évidemment que
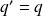 .
.
Et finalement l'unicité du couple
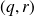 .
.
Exemple :
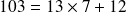 est bien une division Euclidienne.
est bien une division Euclidienne.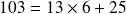 n'est pas une division Euclidienne.
n'est pas une division Euclidienne.
la division Euclidienne dans l'ensemble des entiers relatifs.
Soient
 et
et
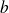 deux entiers relatifs avec
deux entiers relatifs avec
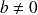 , il existe un unique couple
, il existe un unique couple
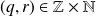 d'entiers tels que
d'entiers tels que
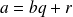 avec
avec
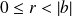 .
.
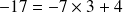 ( division de
( division de
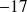 par
par
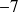 )
)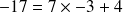 ( division de
( division de
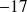 par
par
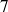 )
)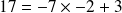 ( division de
( division de
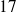 par
par
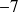 )
)
Fondamental : Divisibilité
Soient
 et
et
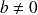 deux entiers tels que
deux entiers tels que
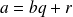 avec
avec
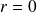 , alors
, alors
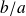 .
.