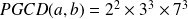PGCD de deux entiers
Diviseurs communs à deux entiers
Les diviseurs communs à deux entiers relatifs sont les diviseurs qui divisent à la fois les deux entiers !
Par exemple :
Les diviseurs de
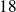sont
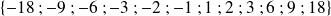
Les diviseurs de
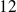sont
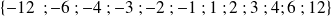
Les diviseurs communs à
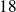et
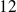sont :
Comme on l'a déjà vu tout ensemble fini d'entiers admet un plus grand élément (même un plus petit).
Ce qui entraîne la définition suivante :
Définition : PGCD
Soient
et
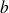deux entiers relatifs non tous les deux nuls. L'ensemble des diviseurs communs à
et
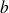est un ensemble fini et admet donc un plus grand élément que l'on note :
.
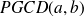Par exemple :
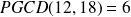
Remarque : Quelques remarques
et
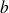sont deux entiers relatifs non tous les deux nuls.
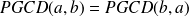et est strictement positif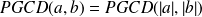
Si
et
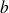sont premiers entre eux alors
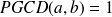
Fondamental : Des propriétés
et
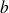sont deux entiers relatifs non tous les deux nuls.
Propriété 1 :
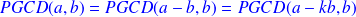où
Preuve :
Il faut démontrer que les diviseurs communs à
et
sont aussi les diviseurs communs à
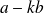et
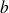. Ils auront donc le même plus grand élément !
Nous savons que si
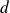est un diviseur commun à
et
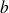alors il divise toute combinaison linéaire de
et
.
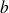Donc tout diviseur commun à
et
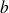est aussi un diviseur de
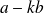et
.
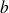Réciproquement si
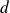est un diviseur commun à
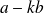et
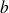il divise
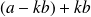, c'est à dire
.
D'où
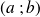et
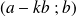ont les mêmes diviseurs communs et donc le même PGCD.
Propriété 2 :
.
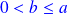
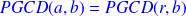
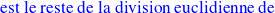
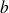Preuve :
On applique la propriété 1 avec
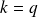où
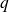est le quotient de la division euclidienne de
par
.
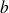Propriété 3 :
.
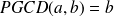Preuve :
On applique la propriété précédente avec
;
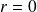Et le fait que
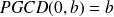car .... allons, un petit effort :)
Fondamental : L'algorithme d'Euclide
Il permet de calculer le PGCD de deux entiers en un nombre fini d'étapes :
Soient
et
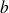deux entiers naturels tels que :
.
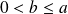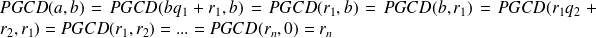
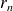étant le dernier reste non nul.
Complément : Encore des propriétés
et
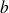sont deux entiers relatifs non tous les deux nuls.
Propriété 4 :
Preuve :
Si
ou
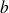est nul ou si
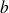divise
, le résultat est évident.
Supposons donc que
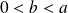; on utilise l'algorithme d'Euclide pour rechercher le PGCD. Et en multipliant les différentes égalités obtenues par
, on obtient :
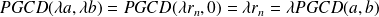
Propriété 5 :
.
Preuve :
Comme
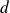est un diviseur de
et
.
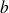On peut écrire que
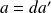et
.
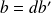D'où :
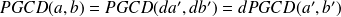
et donc on peut affirmer que :
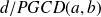
Propriété 6 :
Preuve :
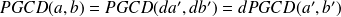
Et comme
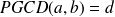
On a :
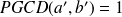
Méthode : Une autre méthode pour déterminer un PGCD
Voyons cela sur un exemple :
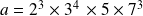
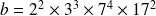
Pour déterminer le PGCD, on prend tous les diviseurs communs avec la plus petite puissance.
