Le théorème de Bezout - Le théorème de Gauss
Fondamental : Propriétés
Soient
 et
et
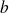 deux entiers relatifs non tous les deux nuls et
deux entiers relatifs non tous les deux nuls et
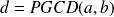
Il existe
 et
et
 entiers relatifs tels que
entiers relatifs tels que
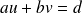 .
.L'ensemble des entiers
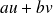 (
(
 et
et
 entiers relatifs ) est l'ensemble des multiples de
entiers relatifs ) est l'ensemble des multiples de
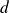 .
.
Preuve : On supposera que
 et
et
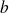 sont des entiers naturels car
sont des entiers naturels car
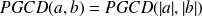
![]()
On fait une recherche de PGCD par l'algorithme d'Euclide : ( on suppose
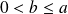 )
)
De
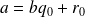 , on peut écrire que :
, on peut écrire que :
 avec
avec
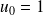 et
et
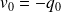 .
.
De
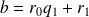 on peut écrire que
on peut écrire que
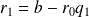 soit que :
soit que :
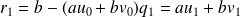
Avec :
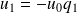 et
et
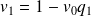 .
.
etc....
A chaque pas on exprime le reste comme combinaison linéaire de
 et
et
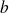 .
.
Et comme le dernier reste non nul est le PGCD, au final on obtient donc :
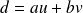 .
.
________________________________________________________________________
Si maintenant on considère un entier
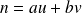 , comme
, comme
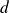 divise
divise
 et
et
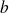 ,
,
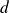 divise
divise
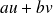 et donc divise
et donc divise
 .
.
 est donc un multiple de
est donc un multiple de
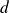 .
.
Réciproquement si
 est un multiple de
est un multiple de
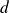 alors il existe un entier
alors il existe un entier
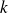 tel que
tel que
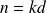 .
.
Comme
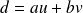 en multipliant par
en multipliant par
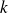 on obtient :
on obtient :
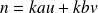 , soit :
, soit :
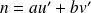
donc tout multiple de
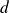 est bien une combinaison linéaire de
est bien une combinaison linéaire de
 et
et
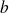 .
.
________________________________________________________________________
 :
:
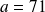 et
et
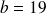 .
.
On a :

Cherchons donc un couple d'entiers
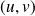 tels que
tels que
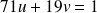 .
.
 ce qui donne :
ce qui donne :
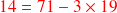
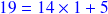 ce qui donne en remplaçant
ce qui donne en remplaçant
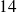 :
:

 ce qui donne en remplaçant
ce qui donne en remplaçant
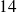 et
et
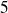 :
:
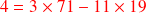
 ce qui donne en remplaçant
ce qui donne en remplaçant
 et
et
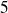 :
:

Le couple cherché est donc :
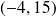
Fondamental : Le théorème de Bezout
Deux entiers relatifs
 et
et
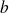 sont premiers entre eux si et seulement si il existe deux entiers relatifs
sont premiers entre eux si et seulement si il existe deux entiers relatifs
 et
et
 tels que
tels que
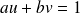 .
.
Preuve :
![]()
Si
 et
et
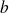 sont premiers entre eux, leur PGCD :
sont premiers entre eux, leur PGCD :
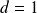 ;
;
Donc il existe bien des entiers
 et
et
 tels que
tels que
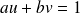 ( propriété précédente).
( propriété précédente).
Réciproquement, s'il existe
 et
et
 tels que
tels que
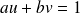 , un diviseur commun à
, un diviseur commun à
 et
et
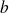 divise
divise
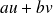 donc 1.
donc 1.
Donc
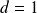 , ce qui entraîne que
, ce qui entraîne que
 et
et
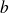 sont premiers entre eux.
sont premiers entre eux.
Fondamental : Le théorème de Gauss
Soient
 ,
,
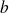 et
et
 trois entiers non nuls.
trois entiers non nuls.
Si
 divise
divise
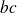 et est premier avec
et est premier avec
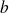 alors il divise
alors il divise
 .
.
Preuve :
![]()
 divise
divise
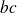 , il existe donc un entier
, il existe donc un entier
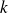 tel que
tel que
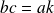 .
.
Comme
 et
et
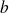 sont premiers entre eux, d'après le théorème de Bezout, il existe des entiers
sont premiers entre eux, d'après le théorème de Bezout, il existe des entiers
 et
et
 tels que
tels que
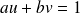 .
.
En multipliant par
 on obtient :
on obtient :
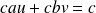 .
.
Soit :
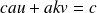 ou encore :
ou encore :
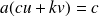
Ce qui signifie bien que
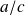 .
.
Méthode : Comment déterminer tous les couples (u,v) tels que 71u+19v=1 ?
Précédemment on a vu que le couple
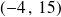 vérifie l'égalité :
vérifie l'égalité :
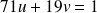 .
.
On dira que le couple
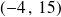 est une solution particulière de l'équation :
est une solution particulière de l'équation :
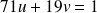 .
.
Nous avons : si le couple
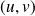 est solution :
est solution :
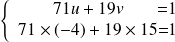 .
.
En égalisant ces deux lignes on obtient :
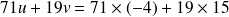 .
.
Soit :
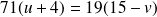
Cette dernière égalité nous permet d'affirmer que :
Comme
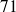 divise
divise
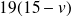 et que
et que
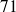 et
et
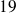 sont premiers entre eux, d'après le
sont premiers entre eux, d'après le
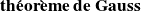 ,
,
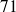 divise
divise
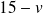 ;
;
Il existe donc un entier
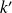 tel que
tel que
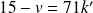 , et donc
, et donc
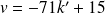 .
.
De la même manière il existe un entier
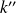 tel que :
tel que :
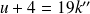 soit :
soit :
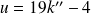 .
.
Réciproquement le couple
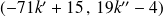 est solution si et seulement si
est solution si et seulement si
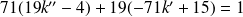 .
.
En développant :
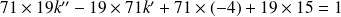
Soit :
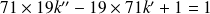
Donc si et seulement si :
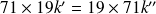 .
.
Autrement dit si et seulement si :
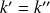 .
.
En conclusion :
En posant
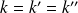 , les couples
, les couples
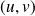 solutions de
solutions de
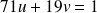 sont les couples :
sont les couples :
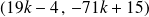 pour
pour
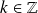
Remarque : Les équations diophantiennes
Une équation diophantienne est une équation du type
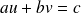 où
où
 ,
,
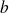 et
et
 sont trois entiers non nuls.
sont trois entiers non nuls.
 et
et
 étant les inconnues .
étant les inconnues .
Résoudre une équation diophantienne c'est déterminer les couples d'entiers relatifs
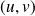 solutions de cette équation.
solutions de cette équation.
On utilise la méthode présentée plus haut :
On détermine une solution particulière :
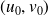 .
.On égalise les deux lignes :
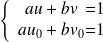 .
.Ce qui donne :
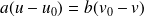 .
.En appliquant le théorème de Gauss on obtient :
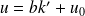 et
et
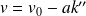 , où
, où
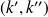 sont des entiers relatifs.
sont des entiers relatifs.On établit la réciproque en précisant que le couple trouvé est solution si et seulement si
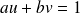 . En remplaçant il vient toujours que
. En remplaçant il vient toujours que
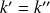 ;
;On conclut.
______________________________________________________________________________

On commence par chercher une solution particulière
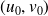 à
à
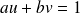 .
.Il suffit ensuite de préciser que le couple
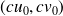 est une solution particulière à
est une solution particulière à
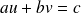 .
.Le reste de la procédure est la même que précédemment.
_______________________________________________________________________________
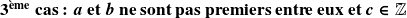
Si
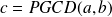 , on simplifie par
, on simplifie par
 et on est ramené au premier cas.
et on est ramené au premier cas.Si
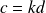 où
où
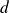 est le PGCD de
est le PGCD de
 et
et
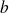 , on simplifie par
, on simplifie par
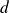 et on est ramené au second cas.
et on est ramené au second cas.Si
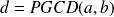 ne divise pas
ne divise pas
 il n'y a pas de solutions.
il n'y a pas de solutions.





