Les booléens
Qu'est-ce qu'un booléen ?
C'est une variable qui ne peux prendre que deux valeurs : VRAI ou FAUX
George Boole (1815-1864) est un logicien, mathématicien., philosophe britannique. Il est le créateur de la logique moderne, fondée sur une structure algébrique et sémantique, que l'on appelle aujourd'hui algèbre de Boole.
On associe 0 à Faux et 1 à Vrai.
Opérateurs de comparaisons
Prenons l'exemple suivant : x= 23 et y = 15
Opérateur | Expression | Signification | Valeur |
|---|---|---|---|
== | x==y | Égal | 0(Faux) |
!= | x !=y | Non égal | 1(Vrai) |
> | x>y | Plus grand que | 1 |
< | x<y | Plus petit que | 0 |
>= | x>=y | Plus grand ou égal | 1 |
<= | x<=y | Plus petit ou égal | 0 |
Les opérateurs booléens
Il existe des opérations spécifiques pour les booléens : La négation, la conjonction et la disjonction que l'on appelle aussi le NON, le ET et le OU logiques
Méthode : Le NON logique
Le NON logique d'un booléen a se définit par :
NON a vaut VRAI si et seulement si a vaut FAUX
On peut définir cet opérateur pas sa table de vérité :
a | NON a |
|---|---|
0 | 1 |
1 | 0 |
Méthode : Le ET logique
Le ET logique entre deux booléens a et b se définit par :
a ET b vaut vrai si et seulement si a vaut VRAI et b vaut VRAI
On peut définir cet opérateur par sa table de vérité :
a | b | a ET b |
|---|---|---|
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Application :
Dans le programme ci-dessous l'instruction ne sera exécutée que si les deux conditions sont vraies
if condition1 AND condition2 :
instructionMéthode : Le OU logique
Le OU logique entre deux booléens a et b se définit par :
a OU b est VRAI si et seulement si a vaut vrai ou b vaut VRAI
On peut définir cet opérateur par sa table de vérité :
a | b | a OU b |
|---|---|---|
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Application :
Dans le programme ci-dessous l'instruction ne sera exécutée que si l'une au moins des deux conditions est vraie
if condition1 OR condition2 :
instructionComplément : Un peu d'algèbre...
Combinons un peu ces opérateurs :
Écrivons la table de vérité de : (NON a) ET (NON b)
a | b | NON a | NON b | (NON a) ET (NON b) |
|---|---|---|---|---|
0 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 0 |
1 | 0 | 0 | 1 | 0 |
1 | 1 | 0 | 0 | 0 |
Rajoutons deux colonnes : NON(( NON a) ET (NON b)) et a OU b
a | b | NON a | NON b | (NON a) ET (NON b) | NON((NON a) ET (NON b)) | a OU b |
|---|---|---|---|---|---|---|
0 | 0 | 1 | 1 | 1 | 0 | 0 |
0 | 1 | 1 | 0 | 0 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 1 | 1 |
On vient de montrer que : a OU b = NON(( NON a) ET (NON b))
Ce qui est équivalent à : NON ( a OU b) = (NON a) ET ( NON b)
Il y a également un parallèle entre ces opérateurs et les opérateurs ensemblistes
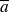 (NON) ,
(NON) ,
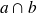 (ET) et
(ET) et
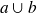 (OU)
(OU)
La formule que nous venons de montrer s'écrit alors :
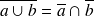 (1ère loi de Morgan).
(1ère loi de Morgan).
Et comme
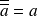 , on a :
, on a :
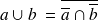
Complément : L'opérateur XOR
a XOR b est VRAI si et seulement si a est VRAI et b est FAUX ou si a est FAUX et b est VRAI
C'est l'opérateur OU- Exclusif, dont la table de vérité est :
On montre que : a XOR b = (a ET (NON b)) OU ((NON a) ET b)
a | b | a XOR b |
|---|---|---|
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
